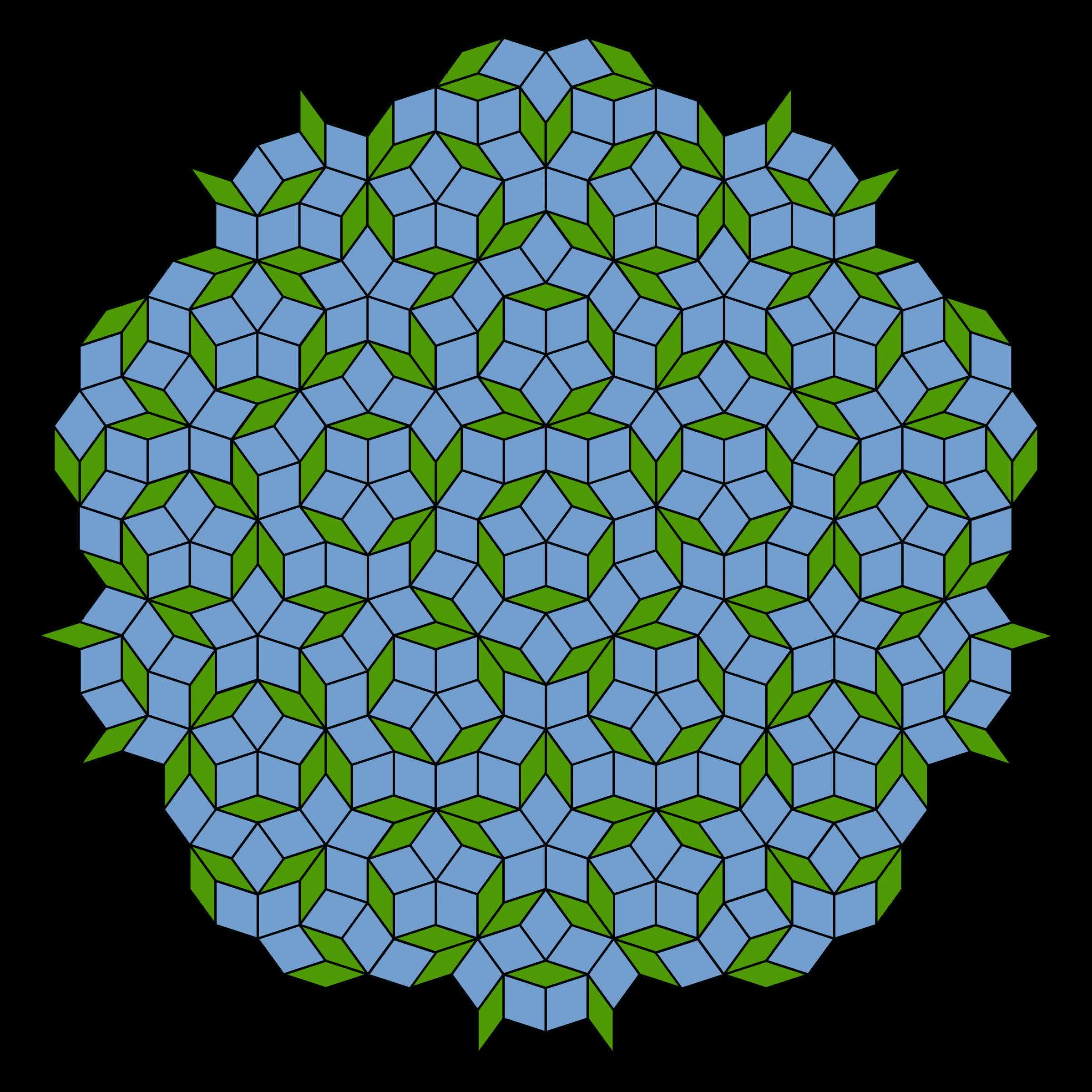
Qu’est-ce qui vient de se passer? Un groupe de mathématiciens a créé un “nouveau” polygone connu auparavant pour n’exister qu’en théorie. C’est une forme à 13 côtés qu’ils ont surnommée “le chapeau”, même s’il n’y ressemble que vaguement. Ce qui est unique à propos de cette figure géométrique, c’est qu’elle peut recouvrir un plan sans créer de motif répétitif.
Le chapeau peut carreler une surface sans créer symétrie de transition. En d’autres termes, le motif résultant ne se répète pas. Il est similaire à la configuration Penrose à cet égard. À première vue, vous pourriez voir ce que vous pensez être un motif répétitif, mais considérez-le de plus près.
Imaginez un sol recouvert de carreaux carrés ou triangulaires. Vous pouvez soulever n’importe quelle section et l’installer sur une autre zone tant que vous ne la faites pas pivoter. Il y a donc une symétrie transitionnelle qui se répète à l’infini. Le chapeau est un oiseau différent.
Tout comme le Penrose, vous pouvez identifier des modèles correspondants à petite échelle. Cependant, imaginez que vous souleviez cette série de tuiles censées se répéter et celles qui l’entourent et que vous les déplaciez pour superposer l’autre motif correspondant – le motif plus petit s’aligne comme prévu, mais en s’éloignant des sections identiques, le reste de la disposition ne correspond pas.
La principale distinction entre le motif Penrose et le chapeau est qu’il ne nécessite qu’un seul prototile au lieu de deux. Ce monotile s’appelle un “einstein” – non pas du nom du célèbre physicien, mais du mot allemand signifiant “une pierre”. Ironiquement, le chapeau est en fait un polykite, ce qui signifie qu’il a été créé à partir de plusieurs formes de cerf-volant, en particulier huit cerfs-volants reliés par leurs bords.
L’existence d’un einstein a été pendant des décennies purement théorique. Les calculs ont prouvé qu’il existait, mais personne n’en avait trouvé jusqu’à présent.

“Vous recherchez littéralement une chose sur un million. Vous filtrez les 999 999 ennuyeux, puis vous avez quelque chose de bizarre, et cela mérite une exploration plus approfondie”, co-auteur de l’étude Chaim Goodman-Strauss, mathématicien au National Museum of Mathematics, a déclaré au New Scientist. “Et puis à la main, vous commencez à les examiner et essayez de les comprendre et commencez à extraire la structure. C’est là qu’un ordinateur serait sans valeur car un humain devait être impliqué dans la construction d’une preuve qu’un humain pourrait comprendre.”
Si vous êtes intéressé par tous les détails mathématiques geek, les chercheurs pré-publié leur article sur le référentiel arXiv de l’Université Cornell. Ils ont aussi un dédié page web avec des informations plus compréhensibles pour les profanes et des exemples d’images concernant la forme insaisissable.